上一篇文章介绍了光响应曲线初始值确定的几种方法,其中,最为稳妥的方法就是采用作图对比的方式,但有小伙伴反应代码量比较大,修改起来容易出错或者看不明白。这也是个问题,因为非线性拟合最难的部分也就是初始值的确定,至于拟合部分,对于统计软件或具有计算功能的软件来讲,只要确定了初始值或其范围,剩下的事情就是交给软件拟合出最终结果,非常简单。因此,为进一步减少光大 LI-6400 和 LI-6800 用户的工作量,我将作图对比法中的程序提取出来,将其进一步完善为本文要介绍的 lrc.start 软件包,以方便 LI-6400 和 LI-6800 的用户来使用。
读取数据的格式
LI-6400 的数据格式要求很简单,表头不要修改,只保留导出 excel 或原始数据文件的表头和测量数据,使用你所掌握的任意方法将数据导入 R 软件即可,必须是 dataframe格式, LI-6800 的要求与 LI-6400 一致,样式分别如下:
LI-6400 数据格式
注:受限于排版的宽度,未显示所有列。
| Obs | HHMMSS | FTime | EBal. | Photo | Cond | Ci | Trmmol | VpdL | CTleaf |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 11:17:23 | 247.5 | 0 | 17.8900448 | 1.2402490 | 363.8494 | 5.676993 | 0.6392769 | 30.79238 |
| 2 | 11:19:53 | 397.0 | 0 | 17.2727385 | 1.0476474 | 361.4220 | 5.257885 | 0.6678402 | 30.84335 |
| 3 | 11:22:23 | 547.5 | 0 | 16.8439480 | 0.8730468 | 357.2621 | 4.793988 | 0.6978914 | 30.88142 |
| 4 | 11:24:53 | 697.0 | 0 | 16.5556909 | 0.8113847 | 356.1285 | 4.563326 | 0.7029185 | 30.89113 |
| 5 | 11:27:23 | 847.5 | 0 | 15.2389528 | 0.6963616 | 353.1639 | 4.217108 | 0.7330305 | 30.95812 |
| 6 | 11:29:53 | 997.0 | 0 | 13.3778973 | 0.6098161 | 354.4347 | 3.912138 | 0.7575295 | 31.00215 |
| 7 | 11:32:23 | 1147.5 | 0 | 10.1900886 | 0.5499567 | 360.2758 | 3.513117 | 0.7415481 | 30.78868 |
| 8 | 11:34:53 | 1297.0 | 0 | 7.4913907 | 0.5044738 | 368.7882 | 3.358474 | 0.7623581 | 30.85906 |
| 9 | 11:37:23 | 1447.5 | 0 | 5.9274311 | 0.4705676 | 371.9833 | 3.538334 | 0.8516160 | 31.33811 |
| 10 | 11:39:53 | 1597.5 | 0 | 3.7266648 | 0.4339196 | 380.2271 | 3.290166 | 0.8492953 | 31.30909 |
| 11 | 11:42:24 | 1748.0 | 0 | 2.9387717 | 0.3849488 | 381.6673 | 2.974796 | 0.8527558 | 31.25271 |
| 12 | 11:44:53 | 1897.0 | 0 | 1.6870850 | 0.2977175 | 384.1619 | 2.755396 | 0.9931319 | 31.70684 |
| 13 | 11:47:22 | 2046.5 | 0 | 0.0214795 | 0.2463256 | 394.1682 | 2.341024 | 1.0034070 | 31.60617 |
| 14 | 11:49:54 | 2198.0 | 0 | -1.3769278 | 0.2015835 | 405.3246 | 2.113570 | 1.0905067 | 31.90278 |
LI-6800 数据格式
注:受限于排版的宽度,未显示所有列。
| obs | time | elapsed | date | TIME | E | A | Ca | Ci | Pci |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1506482783 | 0.0 | 20170927 11:26:23 | 1506482783 | 0.0008851 | 10.3612425 | 386.135 | 171.6695 | 17.37742 |
| 2 | 1506482865 | 82.0 | 20170927 11:27:45 | 1506482865 | 0.0008621 | 10.3346065 | 386.287 | 174.8523 | 17.69907 |
| 3 | 1506482986 | 202.5 | 20170927 11:29:45 | 1506482985 | 0.0008013 | 9.9490963 | 386.775 | 176.6618 | 17.88154 |
| 4 | 1506483106 | 323.0 | 20170927 11:31:46 | 1506483106 | 0.0006955 | 8.9778485 | 388.149 | 176.2576 | 17.83885 |
| 5 | 1506483227 | 443.5 | 20170927 11:33:46 | 1506483226 | 0.0005794 | 7.5754675 | 389.944 | 178.2551 | 18.03889 |
| 6 | 1506483305 | 521.4 | 20170927 11:35:04 | 1506483304 | 0.0005022 | 6.0394698 | 391.955 | 199.7083 | 20.20909 |
| 7 | 1506483425 | 641.9 | 20170927 11:37:05 | 1506483425 | 0.0004196 | 4.9187258 | 393.488 | 207.6760 | 21.01452 |
| 8 | 1506483510 | 726.4 | 20170927 11:38:29 | 1506483509 | 0.0003747 | 4.0239474 | 394.701 | 225.4976 | 22.81878 |
| 9 | 1506483595 | 811.4 | 20170927 11:39:54 | 1506483594 | 0.0003379 | 2.7471387 | 396.215 | 266.6744 | 26.98560 |
| 10 | 1506483676 | 892.4 | 20170927 11:41:15 | 1506483675 | 0.0003094 | 2.0662518 | 397.195 | 289.2526 | 29.26888 |
| 11 | 1506483749 | 965.4 | 20170927 11:42:28 | 1506483748 | 0.0002783 | 0.8054445 | 398.814 | 349.0914 | 35.32387 |
| 12 | 1506483820 | 1036.4 | 20170927 11:43:39 | 1506483819 | 0.0002683 | -0.0551727 | 399.882 | 396.9526 | 40.16528 |
| 13 | 1506483906 | 1122.4 | 20170927 11:45:05 | 1506483905 | 0.0002566 | -0.8092610 | 400.904 | 442.0830 | 44.73083 |
使用方法
首先是软件包的安装,目前放于 github 上
devtools::install_github("zhujiedong/lrc_start")
library(lrc.start)所有的函数都有 LI-6400 和 LI-6800 两个版本,简介如下:
- 直角双曲线模型
plot_nonrec64: 适用于 LI-6400 数据的模型plot_nonrec68: 适用于 LI-6400 数据的模型
- 非直角双曲线模型
plot_rec64: 适用于 LI-6400 数据的模型plot_rec68: 适用于 LI-6400 数据的模型
- 指数模型
plot_exp64: 适用于 LI-6400 数据的模型plot_exp68: 适用于 LI-6400 数据的模型
lrc.start 的实现方法很简单,首先构造初始值的一系列梯度,受限于我的水平,目前直角双曲线和非直角双曲线都是构建 “alpha” 的梯度,例如,假设 alpha 最小值是 0.01,所有的测量值为 13 个,那么 alpha 的变化范围是 0.01 到 0.01 * 13, 以 0.01 为间隔增长,指数模型改变的梯度为 b,变化方式同 alpha,其他数值, Am 以数据中最大的光合速率加最小光合速率的绝对值(也即光强为 0 时的测量值)作为初始值。Rd 以最小光合速率的绝对值作为初始值。具体请看下面的内容。
通过上述方式,构建测量值与计算值的 dataframe(也即测量值与不同梯度参数组成了一个大的dataframe),然后使用 ggplot2 中的 geom_point 和 geom_smooth 做出测量值和所有的计算值的散点图并拟合,尽管拟合使用了非参数拟合的 loess,但由于我们此时的意图是看重合程度,因此,无需确定光合作用的模型,单纯找出重合度最高的参数的范围(也就是在测量值上下的两条曲线所使用的参数值),即可确定初始值范围。
直角双曲线模型
Baly (1935) 提出了直角双曲线模型,它的表达式为:
\[P_{n} = \frac{\alpha I\ P_{nmax}}{\alpha I + P_{nmax}}- R_{d}\]
- 其中,P\(_{n}\) 为净光合速率;
- 为光强;
- \(\alpha\) 为光响应曲线在光强为0时的斜率,即光响应曲线的初始斜率,也称之为初始量子效率;
- P\(_{nmax}\) 为最大净光合速率,在函数参数中我们使用 Am 表示;
- R\(_{d}\):为暗呼吸速率。
实现方式
因为上一篇文章已经展示了 LI-6800 的数据,这里我们使用 LI-6400 的数据作为展示,我们通过 ?plot_rec64 查看其默认参数,演示其基本使用:
# start64 为我测试时的数据,已经内置到lrc.start 内
plot_rec64(start64)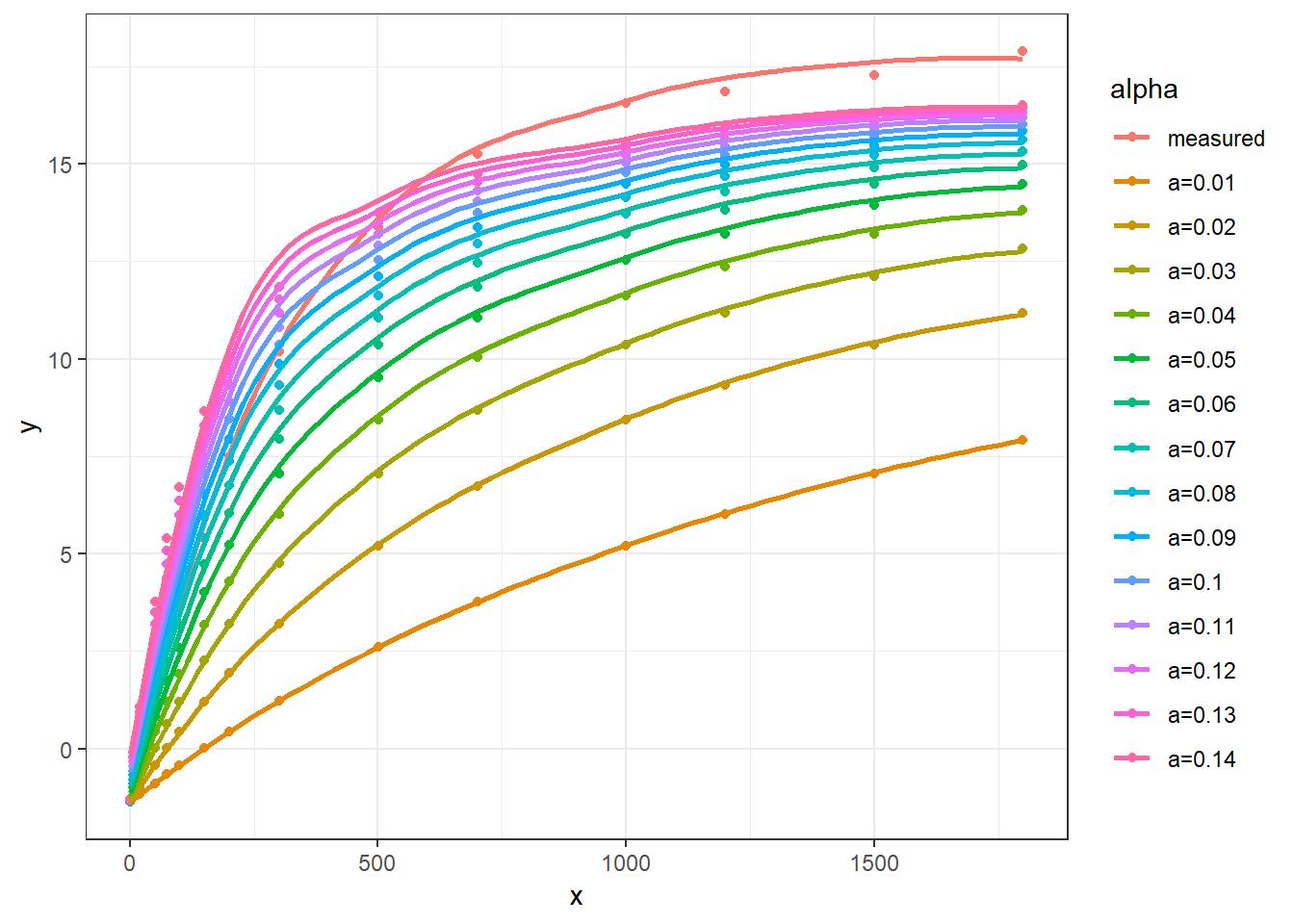
从图中我们可以看到,即使 alpha 取最大值,测量点拟合曲线仍然高于计算值,从表现上来讲,是 Am 值偏低,我们适当增加其值,观察结果:
plot_rec64(start64, Am = 25)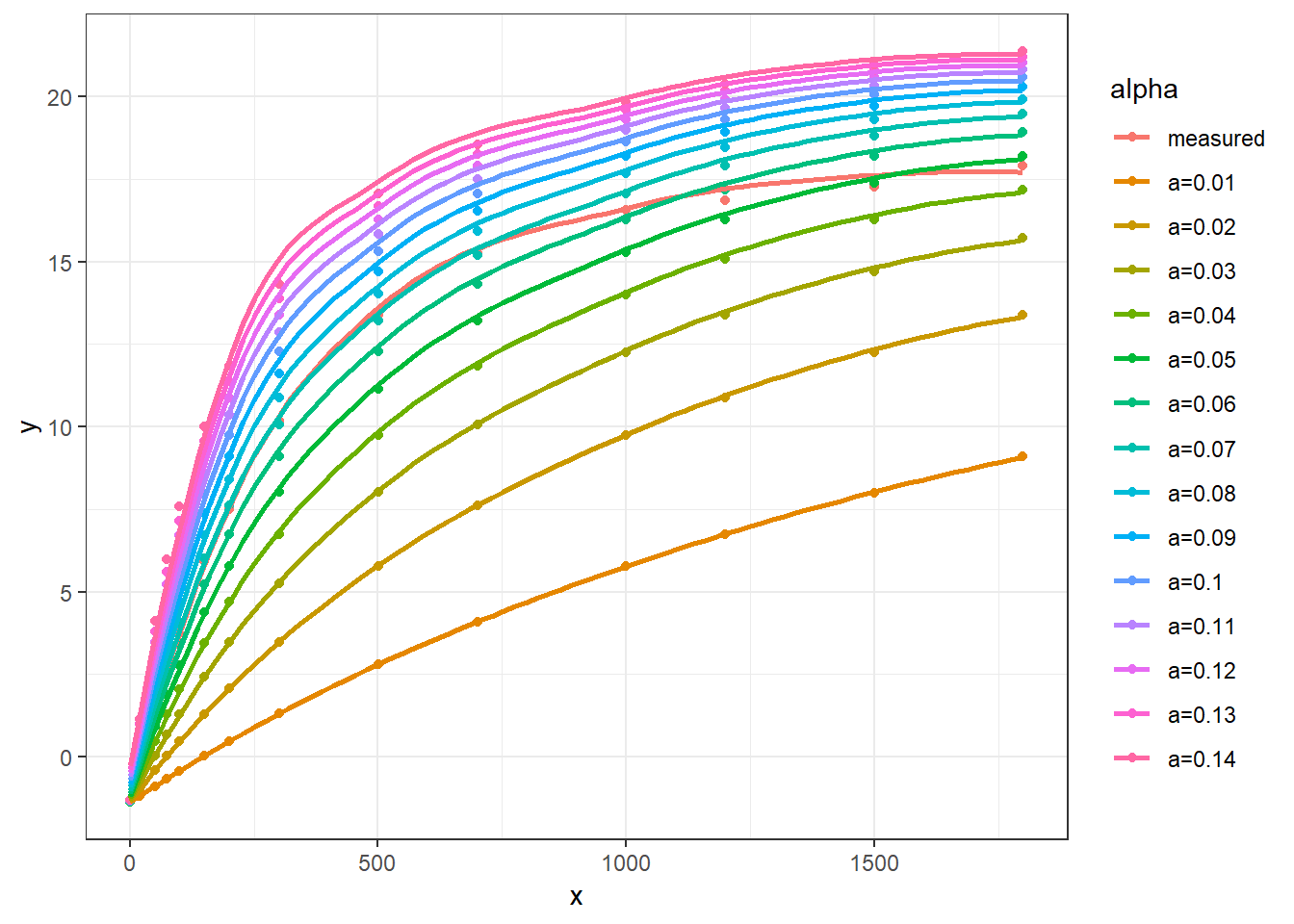
此时看上去测量点与计算点重合程度高于使用默认的 Am 值,看上去 alpha 的取值在 0.06 和 0.07 之间时较为合适,为判断取值是否合适,我们使用最基础的 nls 来验证这种方式是否有效:
lrc_Q <- start64$PARi
lrc_A <- start64$Photo
lrcnls <- nls(lrc_A ~ (alpha * lrc_Q * Am) *
(1/(alpha * lrc_Q + Am)) - Rd,
start=list(Am=(max(lrc_A)-min(lrc_A)),
alpha=0.05,Rd=-min(lrc_A))
)
summary(lrcnls)##
## Formula: lrc_A ~ (alpha * lrc_Q * Am) * (1/(alpha * lrc_Q + Am)) - Rd
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## Am 23.124056 0.357404 64.700 1.49e-15 ***
## alpha 0.078754 0.004846 16.252 4.89e-09 ***
## Rd 1.647967 0.256492 6.425 4.91e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3589 on 11 degrees of freedom
##
## Number of iterations to convergence: 5
## Achieved convergence tolerance: 1.462e-06可以看出,使用 nls 没有报错,初始值判定有效。我们通过简单修改 Am 的值来实现了初始值范围的判断。
非直角双曲线模型
Thornley (1976) 提出了非直角双曲线模型,它的表达式为:
\[P_{n} = \frac{\alpha I + P_{nmax} \sqrt{(\alpha I + P_{nmax})^{2} - 4 \theta \alpha I P_{nmax}}}{2 \theta} - R_{d}\]
其中,\(\theta\) 为表示曲线弯曲程度的曲角参数,取值为\(0\leq \theta \leq 1\)。其他参数意义同直角双曲线。
实现方式
这里我们使用 LI-6800 的数据,作为展示,可通过 ?plot_nonrec68 帮助查看其参数及默认值:
library(lrc.start)
plot_nonrec68(start68)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'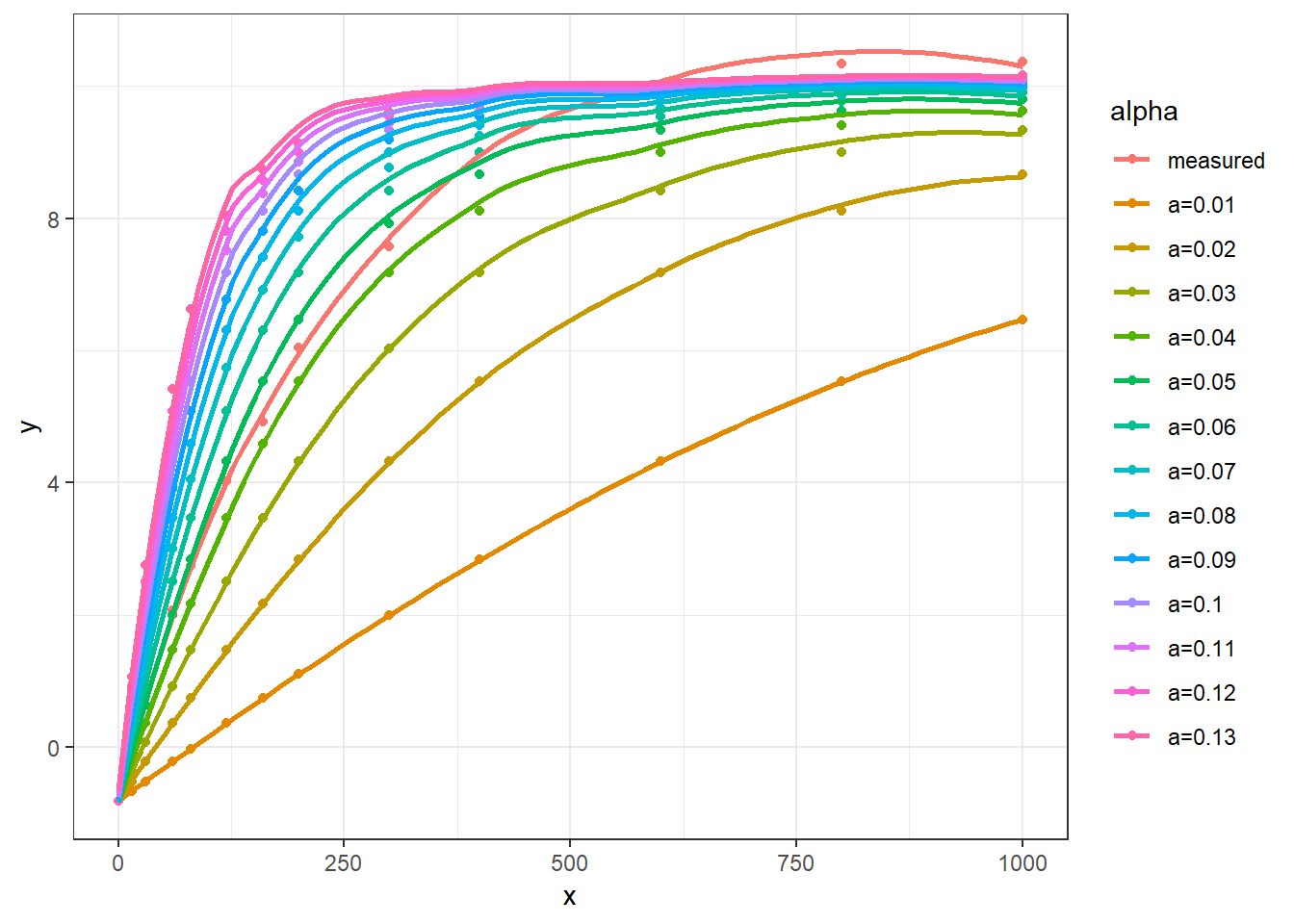
此处曲线大致在 0.4 和 0.5 之间,只不过感觉所有的计算值的光合速率低(前半部分能判断出alpha 在 0.04 和 0.05 之间,但平台阶段值偏低),我们增加 Am值试一下(根据图形来看,Am值设置12左右应该能达到重合度比较高的程度),我们试一下:
library(lrc.start)
plot_nonrec68(start68, Am = 12)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'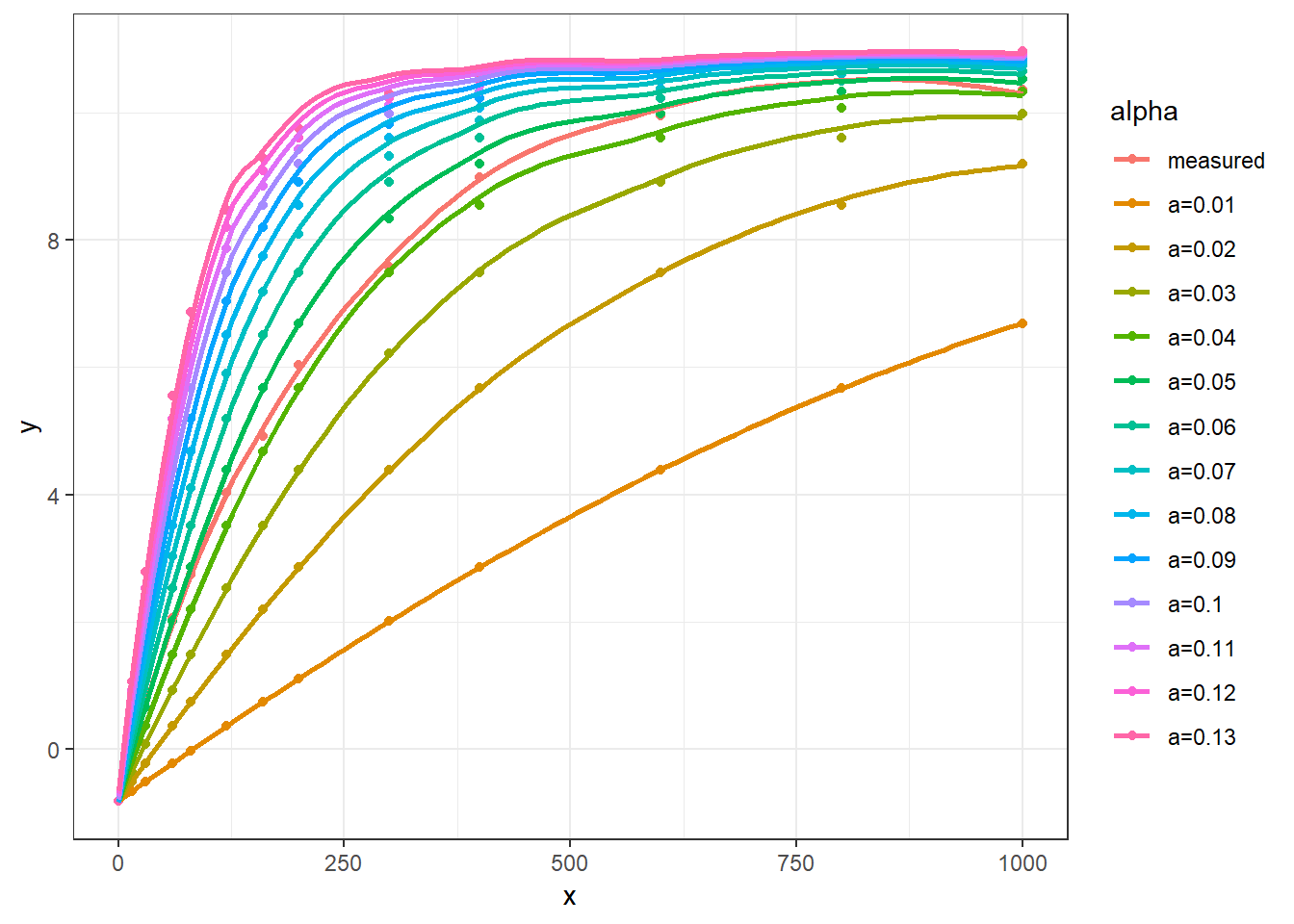
很完美,因为这是上一篇文章所采用的示例数据,因此,就不再用 nls 验证了。
指数模型
光合指数模型较多,我们此处使用的指数函数的模型 Prado and Moraes (1997),其表达式为:
\[P_{n} = P_{nmax}[1 - e^{-b(I-I_{C})}]\]
其中,\(I_{c}\) 为光补偿点,\(e\) 为自然对数的底,b为常数,其他参数意义同。
实现方式
此处我们采用 LI-6400 的数据,我们同样可通过 ?plot_exp64 帮助查看其参数及默认值:
library(lrc.start)
plot_exp64(start64)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'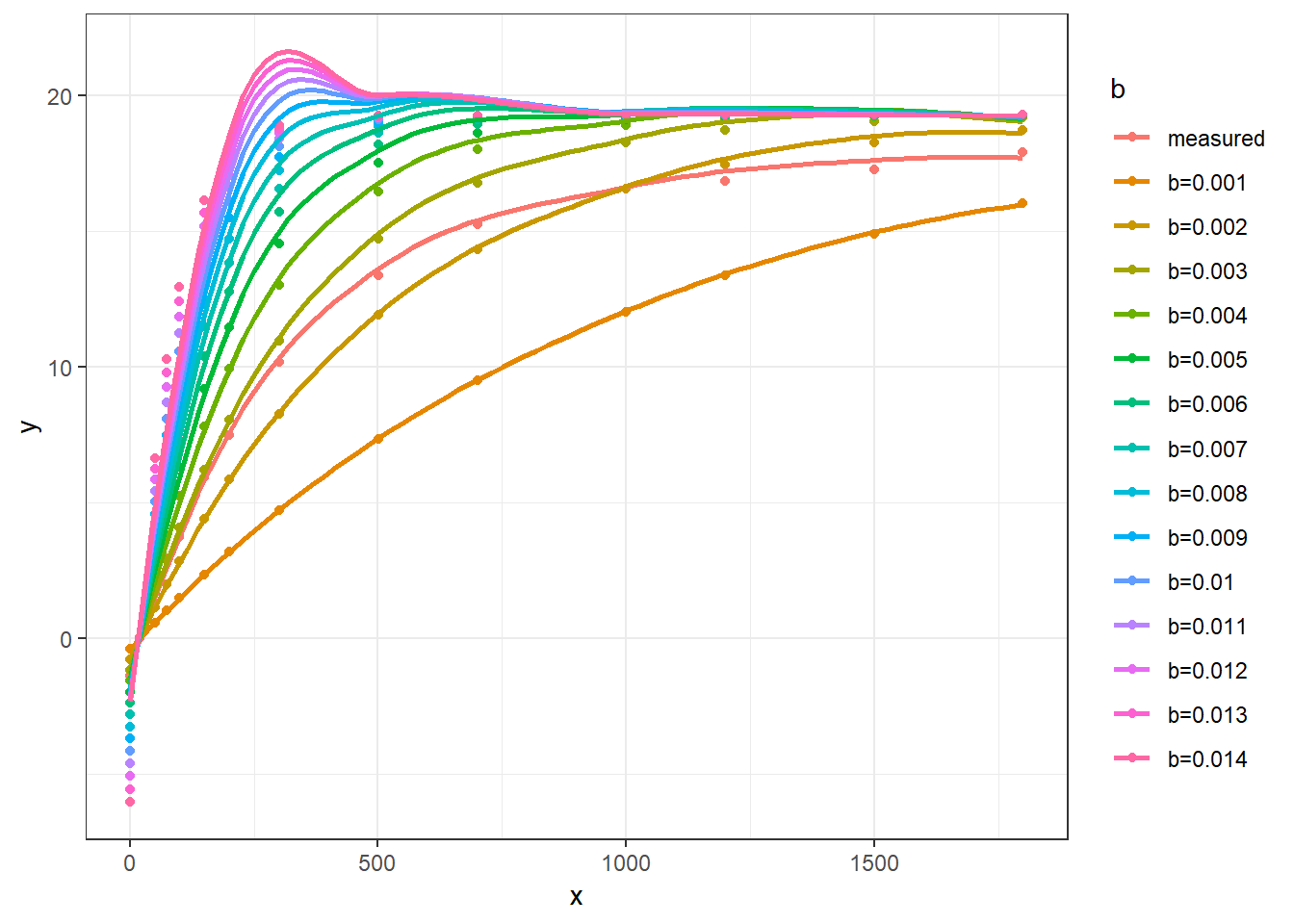
图形看上去有些怪异,但从曲线上判断,b 值大致在 0.002 和 0.003 之间,看上去所有的计算值位置都偏高,我们试着将 Am 减小:
library(lrc.start)
plot_exp64(start64, Am = 18)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'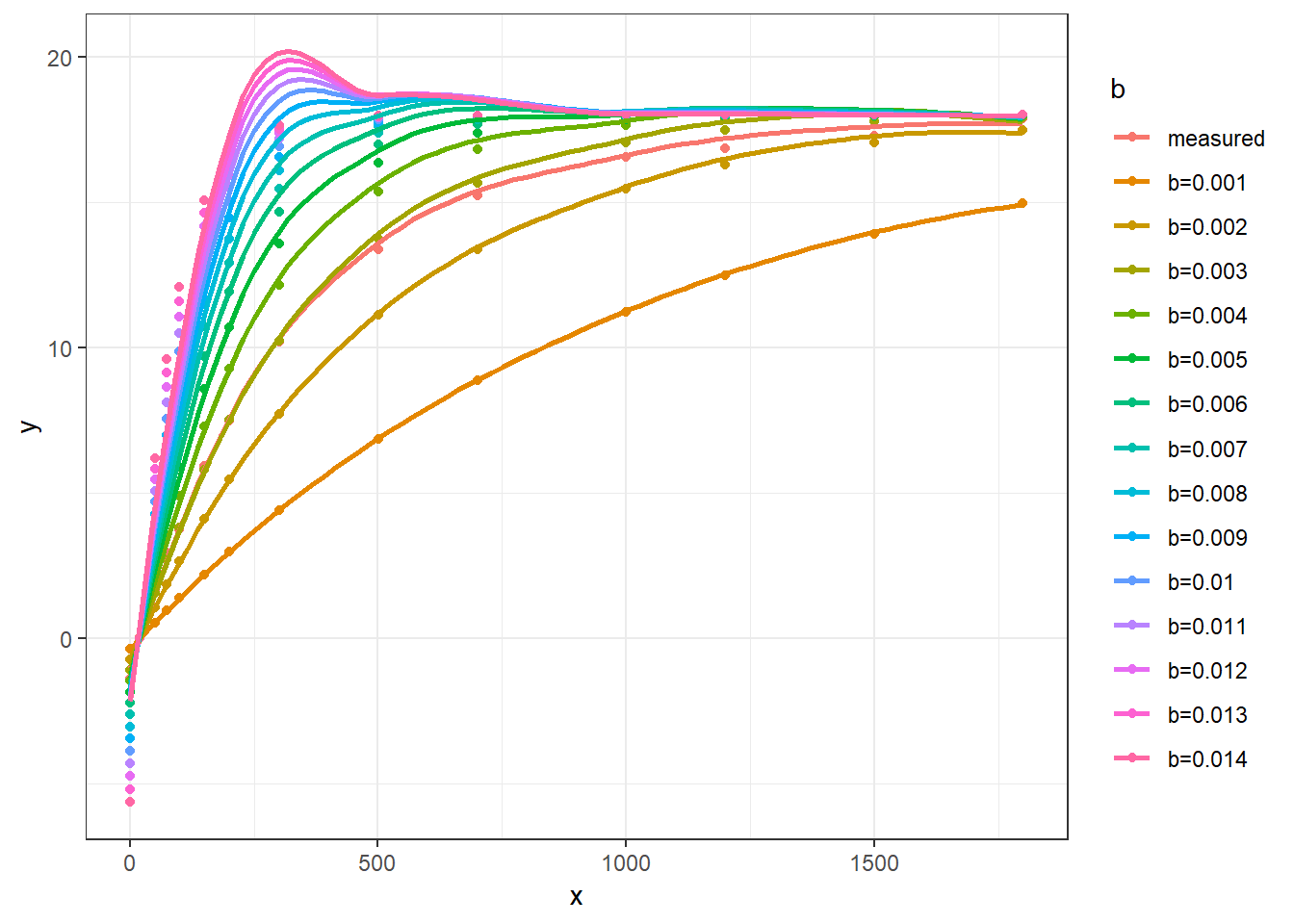
看上去不是太差,我们试着用 nls 来验证一下
lrc_Q <- start64$PARi
lrc_A <- start64$Photo
lrcnls <- nls(lrc_A ~ Am*(1-exp((-b)*(lrc_Q-Ic))),
start=list(Am=18,
Ic=20, b=0.003)
)
summary(lrcnls)##
## Formula: lrc_A ~ Am * (1 - exp((-b) * (lrc_Q - Ic)))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## Am 1.751e+01 1.241e-01 141.154 < 2e-16 ***
## Ic 1.982e+01 2.031e+00 9.761 9.41e-07 ***
## b 3.081e-03 7.833e-05 39.338 3.47e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2122 on 11 degrees of freedom
##
## Number of iterations to convergence: 4
## Achieved convergence tolerance: 2.302e-06小结
忙了几个晚上,终于把 lrc.start 写完并完成了这个并不是特别完整的文档(不是所有的函数都在这里写了,但我写代码的时候是都测试过了,这里确实是偷懒,不想挨着写了,反正每个模型都示例了,感兴趣的童鞋拿自己的数据或我的测试数据自己试一下)。
从上面看出,这个包基本是能运行了,虽然还有不完美的地方,每个模型我只挑了比较关键的参数自动设置梯度,不太关键的参数你只能根据作图结果自己尝试。另外,直角双曲线的修改模型我还没写(这个代码应与其他略有差别,我还没大想好),如果各位有好的思路,欢迎告诉我。
参考文献
Baly E. 1935. The kinetics of photosynthesis. Proceedings of the Royal Society of London Series B (Biological Sciences), 218–239.
Prado CH, Moraes JAPVD. 1997. Photosynthetic capacity and specific leaf mass in twenty woody species of cerrado vegetation under field conditions. Photosynthetica 33, 103–112.
Thornley JHM. 1976. Mathematical models in plant physiology. London: Academic Press.